Qualification Round
简单回顾,本次的Qualification质量说实话还不错 ^ ^!
A. Vestigium (7pts)
给一个矩阵A,检查A的每一行,每一列是否符合元素唯一性,且要求计算一下对角线之和(矩阵的迹)。
思路
送分,就考察一下会不会写代码而已。
B. Nesting Depth (5pts, 11pts)
给一个N长的数字串,要求你给这个串添加括号序列,使得:
- 1)添加后,括号序列是合法的(左括号都有与之匹配的右括号)
- 2)每个数字d所在的括号深度恰好是d(如"(((x))y)z",其中,x的深度是3,y的深度是1,z的深度是0)
- 3)加完括号后,新的字串尽可能短。
举例:
0000 --> 0000
101 --> (1)0(1)
111000 --> (111)000
2013 --> ((2))0(1((3)))
思路
我们看字串中的0,由于其深度只能为0,所以遇到一个0就可以把字符串切成2段。比较容易证明,没有括号能横跨这个0。
借着这个思路,这个问题就可以递归了。f(str, depth)表示求解含有depth<=d<=9的数字的字串的最优解。
剩下的就是coding了,不难。
C. Parenting Partnering Returns (7pts, 12pts)
把一些任务分配给两个人,一些任务在时间上冲突不能同时分配给同一个人。要求给出一个分配方法,使所有任务不冲突。无解的case要return无解。
思路
图染色问题,冲突点连边,点染色为2种,同色点不能相邻。因为只有2种颜色,直接检查能不能构成二分图就可以。
D. ESAb ATAd (1pts, 9pts, 16pts)
给了一个量子数据库,说里面有N个BIT (N<=100)。
有一种Query方式,Query(x) 其中 $1<=x<=N$;返回 当前数据库x位上的BIT,0或1.
但这个数据库有个特性:每Query 10 次,数据库就会发生一次随机波动,以各25%概率发生以下四件事:
- a)所有元素翻转,原来是0变成1,原来是1变成0;
- b)序列反转,$bit[i]$ 和 $bit[N+1-i]$ 对调($1<=i<=N$);
- c)同时 所有元素翻转 + 序列反转;
- d)啥都不变;
你现在对N个BIT一无所知,想在150次Query内,得到所有元素在“当下”分别是什么。
思路
这个问题需要稍微费点脑子,看起来比较复杂,其实不然。
我们把N个元素两两配对,将 $bit[i]$ 和 $bit[N+1-i]$ 组成一对。共$N/2$对组合。
一对数有两种组合方式:
- 1)两个元素相同 00, 11。这个组合在发生事件 a,c时元素会发生反转,发生b,d时不会变化。
- 2)两个元素不同 01, 10。这个组合在发生事件 a,b时元素会发生反转,发生c,d是不会变化。
另外注意,所有1)类型的pair会发生相同的变化,所有2)类型的pair会发生相同的变化。
把Query 10次作为一组。 - 已知的1)类和2)类两个集合中,各检查1个元素就能判断出当前在abcd下的哪种情况。花费2次Query,并update当前两个集合的所有元素新的value。
- 剩下8次可以检查4个没检查的pairs,再把pairs按1)或2)放入对应的集合中。
剩下的就是写代码了,架构越巧妙代码越少。
E. Indicium (7pts, 25pts)
用元素1~N构建一个迹为M的拉丁方阵。($N<=M<=N^2$).
思路
A != C时
A.....
.A....
..A...
...A..
....A.
.....C
是无解的。因为A在N那行是没地方放的。所以$M=N+1$ 或 $M=N^2-1$是无解的。
A.....
.A....
..A...
...A..
....A.
.....A
A!=B 时
A.....
.A....
..A...
...A..
....BA
....AB
A!=B and A!=C and B!=C 时
A.....
.A....
..A...
...A..
....BA
....AC
都是有解的。其他的M都可以构造出这样形式的对角线。
构造可以借助二分图最大匹配来辅助构建还没填的位置。
Round 1A
参加的这场,代码有些生疏,在A和B上花费了太多的时间,导致没有时间写C。快速写了C的小数据,以保证能进下一轮。
A. Pattern Matching
字符串的表达式中 * 可以匹配任意的子串(包括空串)。给出一个若干个表达式(>=2个,<=50个),这些表达式只含有大写字符和*,求找到一个字符串能同时匹配所有的表达式。如果不存在输出*
例如:
inputs
H*O
HELLO*
*HELLO
HE*output
HELLO
思路
比赛时采用的方案是:
两两贪心merge,生成一个包含两者特性的表达式,过程使用了 动态规划。最后把最终的表达式里的*用空串替换即可。不过代码比较长。
之后看了一眼分析,发现还有更简单的方案。
利用几个特性:
step 1:
如果表达式有前缀或后缀,直接选择所有pattern中最长的前缀和最长的后缀分别去匹配所有的pattern,如果这都不满足,肯定无解。如果都能贪心的匹配上, 进行下一步构造。
step 2 (这里用了一个比较巧的特性):
贪心匹配完并改造后的pattern一定满足形式:
PREFIX * SUFFIX
PREFIX * WORD * SUFFIX
...
PREFIX * WORD1 * ... * WORDn * SUFFIX下面你要做的就是找出所有的WORD把它们按任意顺序连接起来塞在PREFIX与SUFFIX之间即可。
为什么?可以自己画画就知道了。
B. Pascal Walk
你一开始位于Pascal三角(杨辉三角)的顶点格子(最上面的格子)。每一次你可以从当前的位置向周围6个格子走一步。希望你能在500步内,走出一条轨迹,使轨迹上的数之和恰好等于N($1<=N<=10^9$)
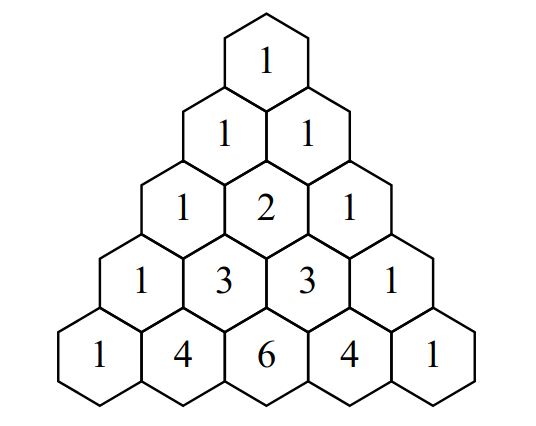
思路
这里可以利用Pascal三角的一个特性:其第$i$行(0-based)的和恰好为$2^i$。
粗略的idea就是这个数的二进制表达下的第$i$位为1,那么我们就把第$i$行走一遍。不过由于我们不能凭空从第$x$行跳到第$y$行,所以需要预留一些数值用来切换行(沿着最左边或最右边走,达到换行的目的)。显然预留32步就足够了,那么约定 $N-32$ 的二进制数第$b$位是1,那么就把$b$行走一遍,对于是0的位,沿着左边或右边往下面一行走。最后未使用的数值在最左边或最右边往下走用1填充完。
那么如果 $N<32$ 呢?直接沿着右边界走N格即可。
C. Square Dance
RxC的网格,每个网格里有一个数值为 $S(i, j)$ 的舞者。接下来会进行N轮比赛,每轮比赛结算后会有若干个舞者被淘汰。一个舞者会不会被淘汰,其规则如下:
一个舞者上下左右方向上最近的其他舞者(可能是0~4个)的数值的均值为$A(i, j)$。 如果 $S(i, j)<A(i, j)$ 那么这个舞者被淘汰。
如果一轮比赛结束时,没有任何人被淘汰,那么整个表演结束。
整个表演的精彩值等于所有比赛的精彩值之和。而每场比赛的精彩值又等于这场比赛开始时,所有舞者的数值之和。
给定S矩阵(1 ≤ R × C ≤ 1000)求整个表演的精彩值。
思路
假设我们有数据结构维护每个人上下左右最近的其他舞者分别是谁(比如链表)。
注意到没删除一个人,只用更新最多4个人的状态。所有暴力也是$O(R × C)$的复杂度而已。
Round 1B
这场相对于前面那场,似乎多了一些分析的要求,代码反而少了。
A. Expogo
你初始在 (0,0) 想去 (X,Y)。你的移动方式:
- 每一步可以向上下左右四个方向之一,移动一步;
- 第ith步(1-based,即ith=1,2,3,...)你移动的步长是 2^(ith-1);
若干步后如果可以到达,则输出每一步的方向。如果不能达到,输出 IMPOSSIBLE。
思路
乍一看是一头雾水的,如果爆搜,每一步有4种可能,显然会TLE。
但是自己代入几个例子后,就能发现其中的trick。
假设:已经规划了n步,已经在位置(xn,yn),下面准备走第n+1步。
令 x' = X - xn, y' = Y - yn。
什么情况一定无解?显然以下情况之一:
- x' % 2^(n+1) != 0 or y' % 2^(n+1) != 0. (直接不能整除,因为再往后,除数越来越大)
- x' / 2^(n+1) and y' / 2^(n+1) are both odds or both evens. (两个方向都是奇数,或都是偶数,因为,只能提供一个2^(n+1),且也必须提供一个2^(n+1))
所以,不难发现,如果n步已经确定,那么n+1步是左右还是上下是确定的。所以每步只有2种走法!
但是似乎这样还是会TLE!
但是注意到另一个细节,如果当前2种可能,我们选了一个发现选错了。那么在n+2步时会立马发现有问题!所以大胆的尝试即可,错了也只会多搜一层而已。
如果是搜索的方法,注意一点:因为最后一步的时候,一定是2^k的形式,所以走反了,下一次是2^(k+1)依然是合法的。这就需要及时的停止才行。
B. Blindfolded Bullseye
在宽2×10^9纳米,长2×10^9纳米的墙上有一个半径为R的靶子。这个靶子的中心在一个整点上,靶子的半径R在A~B之间(A=10^9/2, B=10^9)。
但是这个靶子对你是不可见的,你又想知道靶心在哪。
你可以做的操作是:
- 向整点(x,y)的点扔一个飞镖,必然能命中。系统会返回你3种结果:
- MISS: 飞镖落点(x,y)在靶子外;
- HIT: 飞镖落点(x,y)在靶子内,但没命中中心;
- CENTER: 飞镖落点(x,y)就是靶子中心;
你需要在300次操作内,命中一次靶心。
思路
很容易就能意识到一个关键点: 如果我们能随机命中任意靶子内的一个点,如P点(xp,yp)。
那么我们有log级别的方法找到中心。
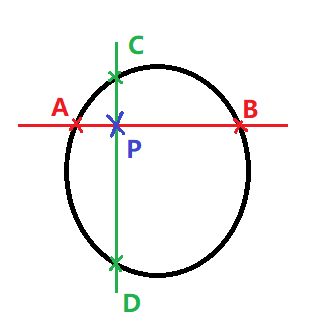
从最左边点和P间的直线上,可以二分出圆内最边界的整点A;
从最右边点和P间的直线上,可以二分出圆内最边界的整点B;
同理可以获得上边界的点C,下边界的整点D。
AB的中点获得圆心的x,CD的中心获得圆心的y。
那么如何获得园内的任意一个点P呢?
注意半径R>=10^9/2.所以可以把空间划分出8x8=64的网格,检查每个网格的中心。必然有一个会落在圆内的。
C. Join the Ranks
一副特殊的牌,有R种数字,S种花色。共RxS张牌,每个pair各一个。
一开始按花色排好序,每种花色内再按数字大小排好序。所以数字上看,这副牌从上往下是:
1, 2, 3, ..., R, 1, 2, 3, ..., R, 1, 2, 3, ..., R, ..., 1, 2, 3, ..., R.
你要做的是把这副牌重组一下,使其按牌的数字大小排好,花色无所谓什么顺序,即变成:
1,1,1,1..,1,2,2,2...,2,3,3,3,...3,....,R,R,R, ...,R.
这里的一步操作,有三小步完成:
- 从牌堆选出最上面的A张牌,组成的牌堆,SA
- 再从剩下的牌堆中选出最上面B张牌,组成的牌堆,SB
- 将SA放回剩下的牌堆的上面,再把SB放到SA的上面。
问最少多少步操作能完成这个排序任务。
思路
如果我们把每张牌作为图中的点,其和其后面的一张牌连一条边。那么任意一个排序都是一个 $R*S-1$ 条边的图.
最终状态我们希望的图状态是 对每个i,有S-1 条 i->i的边,有一条 i->(i+1)。
而一次操作最多可以改变两条边。
贪心的思路,每次都改两条边,实在不行就改一条。
但是非常幸运的是,这样就可以了。。。 :)
提示:可以证明如果多于2个没有被还原的边,那么至少可以找到一个方法还原2条边。细节就不写了。
Round 1C
Round 1 最最最简单的一场。可能是考虑到大部分的大佬都已经晋级,所以难度降低了很多,来适配大部分的选手。
A. Overexcited Fan
你在街道(0, 0),你的偶像在(X, Y)。你想要的他的签名。每一回合,你可以往上下左右走一格,或者你可以选择站在原地。
你的偶像每回合也会往上下左右走一格,不过幸运的是,你知道他未来的每一回合会往哪走。
问最少多少回合你可以和偶像在同一个位置。
思路
第i回合你的偶像在(xi,yi),那么如果abs(xi)+abs(yi)<=i那么你一定可以在i回合到达这个点。
枚举i即可。
B. Overrandomized
有一台随机数发生器服务器。你每次query一个数M,那么这个server会返回一个1~M之前的随机数。
不过这个服务器做了一个加密操作,它会把0 ~ 9这10个digit,替换成10个不停的字符,这是一个双射。由于忘记了每个数字对应的字符是什么。(比如0123456789 -> BVCXZASFDG. 那么VFB就是170)
所以你准备测试一下,你用了10000个随机的M(M在1 ~ 10^U-1之间),获得了10000个回复,当然是10000个字符串。
返回0~9对应的字符
思路
注意到最高位是不可以是0的,所以我们可以看首字符和末字符的集合,末字符集合存在但在首字符不存在的那个字符就是0.
对于其他的数字,我们意识到9会最少出现,因为M必须以9开头,U长的字符才可能随机到9开头。
同理8第二少,1最多。
所以对首字母频率排序,即可得到结果。
C. Oversized Pancake Choppers
你有N张饼(N <= 10000, size分别是A1,A2,...,AN, Ai是整数 1<=Ai<=360 x 10^9).
有D个顾客(D <= 50).你要做的是提供给每个顾客一张饼,且每个顾客的饼恰好一样大。
这些顾客不care自己拿到的饼多大,他们care的是自己拿到的饼是不是和别人的饼一样大。
因为也许A1 ~ AN中没恰好D个一样大的饼,所以你需要切一些饼来满足这个条件。一个A大的饼,你可以一刀切为X和Y大的饼,A=X+Y。注意:X和Y都不需要是整数。然后你还可以对X或Y继续切。
问:你需要最少多少刀来完成这个任务。(显然这个答案不会大于D-1,因为你可以把一个饼切成D份,D-1刀均分,来满足所有人)
思路
首先,我们很容易意识到最优解对应的饼尺寸一定是 某个 Ai/k (Ai属于N个饼的集合,1<=k<=D).
$D*N$ 种可能。
但是知道了尺寸,怎么知道这个尺寸最少需要多少刀切出不少于D个这个尺寸的饼呢?
part1:
首先,选出恰好这个尺寸的饼,因为不用刀。
然后,如果一刀出2个,就选一刀出两个的。
然后,如果2刀出3个,就选两刀出3个的。
....
part2:
如果没有整除的情况,那么我们再选那些不能整除的情况,一刀出一个。
用map和排序的序列,我们很容易模拟上面的过程。因为D<=50所以不用担心模拟不完。
对part1,最多枚举到D-1刀出D个的情况。
对part2,因为一刀多一个,所以只要测试不超过D张饼即可。
所以模拟2D次。
总O(D^2 * N)
下面简单说明这个贪心是对的。
显然part2是对的。
为什么part1是对的?
这里我们发现省的刀都是整除的那些饼,最后一刀出2个带来的。所以一刀出2个的次数越多,总次数越少。
先切小的饼,显然更容易提前出线一刀出2个的情况。
Round 2
A. Incremental House of Pancakes
两堆饼,分别堆着L和R个饼。之后会有源源不断的订单,第i个订单会买i张饼(i从1开始)。
当接到一个新的订单后,我们会从两堆饼中找出多的那堆取出i张饼送出(一样多从左边那堆拿)。如果一个订单下达后,最多的那堆饼的数量不够,那么直接结束。
现在给定L和R,问能卖多少个订单,结束时左右各剩多少饼?
思路
这里需要发现规律:流程走到一定程度后,一定会出现第k单从左拿,k+1单从右拿,k+2单从左拿,k+3单从右拿...直到结束。
证明:假设第k单起出现第k单从左拿,k+1单从右拿。不妨设第k单时,d(k)=L(k)-R(k)。显然有 0 <= d(k) < k(否则k+1一定还从左拿).那么k+1单完成时L(k+2)=L(k)-k, R(k+2)=R(k)-k-1. d(k+2)=L(k+2) - R(k+2)= d(k)+1, 显然有 0 <= d(k+2) < k + 2. 数学归纳可证。
OK,剩下的就是分段求和了,不会的话二分也行。。。
B. Security Update
一个网络,需要从一个起点向外更新一个补丁。更新的过程,一个收到补丁的网络节点会立刻向直接连接的其他节点广播补丁。连接节点收到更新的时间取决于两个节点之间的连接延时(这个延时是一个整数秒)。从一个源节点开始,等待一些时间后整个网络就会全部更新。
由于工程师想复原一下每个节点的更新延时时间。于是他们去查找一些日志,但是对于每个计算节点,能获得的信息只有两种类型之一:
- 知道这个节点是什么时间被更新的(秒)
- 知道这个节点在整个网络中是第几个被更新的(第一次收到补丁时的排序)
给出网络的拓扑图,轻给出一种延时时间的方案,满足上面所有日志。(source node始终是1,它的更新时间始终是0时刻)
思路
对于知道延时的节点,就用给定的时间。其实这个问题需要解决的只是那些有rank序的节点应该设置多大的时间?
虽然有点绕,但是思路还是很容易发现的。我们把节点按给出的信息类型分成两组,然后各自排序。然后我们从1号node开始依次去确定下一个被更新的节点。显然这个节点必然是rank队列或者update time队列的队首成员。那么是谁呢?
我们不难发现 rank队列的rank值是可以做推断的,比如现在确定了k个node,如果下一个是rank序列的成员,那么它必须满足rank(elem) <= k + 1. 不满足就从update time队列拿出下一个成员。
如果从rank队列出来,那么应该给他什么time呢?显然越小越好!找到已经确定的成员,和其相邻的最小值timei,以及当前已知最后更新的时间timej,最优time=min(timej+1,timei+1)
模拟即可(注意相同rank的情况,time要一样)
C. Wormhole in One
空间有N个洞,已知这些洞可以设置配对关系。如果洞A和洞B设置了配对关系,那么一个速度(vx,vy)的球落入洞A会立刻从B出来,再以(vx,vy)继续前进。同理如果从B进来,也会以同样的速度从A出来(类似传送)。但是一个洞A和B匹配后,A和B不再能和其他洞匹配。
现在你可先把N个洞的配对设置好(传送门设置好),也可以不设,落进去就没了。
然后你可以把一个球放在任意位置以任意速度打出,目标,让球经过的洞尽可能多。(从A进从B出,就算经过A和B了,但是多次进A只算一次)。
思路
因为速度不变,所以需要枚举速度的,O(N^2)种可能,速度方向确定后,沿着这个方向把共线的洞连起来。如果一个线上有>=2个点,那么一定有办法让球进入其中一个,然后经过每个洞再传送到另一根共线的线上。
证明:偶数比较容易A1出,A2进,..., A2n-1出,A2n进,去另一根线。奇数怎么办?乍一看奇数好像需要浪费一个洞,其实不然,我们可以拿两根奇数线来配合,以3个点举例(其他也一样),另一根线X的与A2连接,A2出A3进A1出A2进X出。等于从X进的球又从X出来。如果只有奇数个奇数线那就不能玩了,必须浪费一个。
最后注意还能带最多2个只有1个点的线。
D. Emacs++
(没做)
Round 3
只做了一题就想睡觉了。
A. Naming Compromise
两个词A,B,求一个新词C。使max{Dist(A,C), Dist(B, C)}最小。
Dist是编辑距离。(距离有一些规则,这里就不叙述了)
思路
很容易发现min(max{Dist(A,C), Dist(B, C)} | C=ci) = ceil(Dist(A, B) / 2).
这样就简单的,我们先求A到B的编辑距离,DP。然后试图去把A改成B,然后只要改一半,那么就是C。
(未完 ~ ~ 有空再写)
总结
太久不刷真的刷不动了,经常卡成狗~~ 勉强能进R3已经很幸运了